Bruce Li
COSMOS 2023
Cluster 5
Week 1
Monday, July 10
ACADEMIC
How was your (first?) experience with Linux and the Linux workstations today? We talked about Graphical User Interfaces and Command line interfaces? What do you see as the value of each type of interface?
PERSONAL
It's been over 24 hours... What has been the best and most challenging aspect of living at COSMOS?This isn’t my first time using a Linux based OS, and I had a decent amount of experience working with it in the past. CLI and GUI both have lots of different uses for different applications. CLI is useful for experienced users who need to quickly issue commands to get things done, and can be quite powerful in the right hands. GUI on the other hand can also fit that use, but it’s easier to navigate and identify different things.The best thing so far is definitely all the friends I made. Everyone is super nice, and I made a lot of friends with people in my cluster as well as those in the dorm. The most challenging thing I would say is getting the keycard to work on the first swipe. A close second would be managing the heat, since it's cold enough for jackets in the mornings but over a hundred degrees coming out for lunch.
Tuesday, July 11
Speak to a COSMOS student from another cluster. Reflect on what you learned from them by asking them questions like:
1. What is the most interesting thing you learned?
2. Teach me a concept that was new to you.I talked to my roommate in cluster 7, which is introduction to plant microbiology. They’ve been getting into some research, and have already started planning their final project topic and presentation. One of the most interesting things he learned was that there are different microscopes that can produce both 2D images (top down) as well as 3D images. A new concept that he taught me was symbiosis, which is where two unrelated organisms live closely and interact together. There are 5 types of symbiosis, and they can be represented with emojis:
Mutualism: both organisms benefit from the relationship (🙂🙂)
Commensalism: one organism benefits while the other is unaffected (🙂😐)
Parasitism: one organism befits at the expense of the other (🙂😥)
Amensalism: neither benefits, but one is harmed (😐😥)
Neutralism: neither are affected (😐😐)
Wednesday, July 12
“How do you know you understood a lecture?” - Dad-del
Reflect on Dr. Dad-del’s question above.The best way to know if you understood a lecture is by teaching the content to someone else. It allows you to reinforce the key points and the structure of the hierarchy of the presentation (from the book!). By teaching it, you have to fully understand and explain the topic, only something that you can do if you are able to remember and connect the different parts of the lecture together into a coherent structure that you will then teach to the others. Teaching others also gives you the opportunity to consider questions that might not have come up during the lecture. These questions allow you to think more and make connections, which can also deepen your understanding of the lecture.
Thursday, July 13
“What at the Academy of science could possibly be connected to a robotics project? What’s something interesting that you saw that inspired you to look further into it?”One thing at the californa academy that could be connected to a robot project could be the earthquake simulator. It may be veering more toward architecture and is all pre-programmed, but a robot could be made to test out the stability of small scale model buildings. It could use 3 motors moving randomly to simulate the 3 dimensional movement during an earthquake (the simulator at the academy was only able to do two dimensional, no vertical movement). Their website didn’t document how the mechanisms that shook the house worked, or maybe I didn’t search enough, but it did include interesting information about some of the interior things, about how the books foreshadowed the earthquakes and the fishbowl with mineral oil.
Friday, July 14
ACADEMIC
Describe your comfort level working with the motor commands (Robotics) and working with strings (BioPhysics) before and after today. Are there any concepts already discussed in our courses that you feel you need to ask more questions about before the start of week 2?
PERSONAL
Reflect on how cognitive illusions could challenge (or already has challenged) your learning.I’m pretty comfortable working with motor commands, but not to the point where I can remember every function and what they do. I still have to refer to the docs for the function names and parameters, but I’m pretty confident using the functions and dealing with the values like speed and the encoder settings. Before coming into this course, I had some prior experience in python, so I’m comfortable with working with strings. I knew all of the methods and different ways to work with the strings except for the one to reverse it ([-1::-1], starting from the last one and incrementing the index by -1 every time, thus reversing the string). I’m fairly confident with the topics that were covered, but there are things out there that I haven’t learned.
Cognitive illusions definitely played and will play a big part in my learning. It could hinder our ability to learn by tricking us into thinking that we already know the topic that is being discussed, thus preventing us from learning.
Week 2
Monday, July 17
ACADEMIC
What were some new coding concepts in Python (such as dictionaries, tuples, etc) that you learned and how do you think you might use them in your own project?
PERSONAL
Reflect on the story of the stones from Dr. Dad-del. How have you already (or will) applied the message to your own life? Consider how you may have your own story to tell Dr. Dad-del if you ran into him in the hall.All of the coding concepts were the ones I had already known, and along with all the reviews (it's been a while since I last used python), I will definitely be incorporating these concepts into the project. Lists are a must have for storing data, especially ones that result from a timeline. Tuples aren't that really useful, and the main use of them is to serve as keys for dictionaries, which will definitely be used a lot for keeping track of pairs of data (like coordinates).
The story about the stones really made me think: if he would be both happy and sad (happy because it turned into precious stones, but sad thinking that he should’ve gotten more), but completely filled his pockets with the pebbles, would he still be sad? I feel like this story definitely relates to learning and studying. Our parents and the teachers are like the voice telling us to pick up the pebbles, which would be skillsets or knowledge. We may feel annoyed, but they will eventually turn into precious stones that will help us greatly. By then it would be too late to pick up more pebbles, so I feel like the message here is to seize the moment to study and gather as much knowledge as possible so as not to regret it later.
Tuesday, July 18
ACADEMIC
While working in the lab today, what was a new concept you learned about coding and/or robots today?
PERSONAL
When you encounter frustrating situations that are beyond your control, how do you deal with it? Do you feel you usually handle it well or do you frequently let it “get to you”?Today during the robotics lab, I discovered a setting for the IDE (under windows: beginner, advanced, and another one that I can’t remember) that gave more documentation on more commands. It was really convenient and gave lots of information on the different commands that we haven’t used yet. I will be looking into these commands more when working on the project.
It usually depends on what the context and scenario is. Usually I would try again, but sometimes I would give up and come to it again later. I feel like I handle it pretty well most of the time, but there are definitely times when it does get to me.
Wednesday, July 19
Explain how negative numbers, complex numbers, and floating point numbers are represented with ones and zeros (if you know). If you do not know, develop your own system to represent these numbers.
PERSONAL
What news tips did you pick up today to help you study and prepare for tests?I might not remember completely, but how these numbers are stored are as follows: negative numbers use 1 bit in the very front to represent positive or negative (positive is 0 and negative is -1). I’m assuming complex numbers would separate the bytes into halves and store the real component and the imaginary component in the other. For floating point numbers, I think it’s stored as an exponential form, and I vaguely remember something about the mantissa.
The most I took away from the test taking presentation was about reviewing for the test, especially the phrase that “memory is the residue of thought”. This means that you cannot simply just read or go over notes mindlessly and expect to remember them for the long term. Instead, connections must be made to ensure that the memory is cemented.
Thursday, July 20
ACADEMIC
1. How do computers represent floating point numbers like pi? Why is this important to keep in mind?
2. When should you use a list and when should you use a numpy array?
PERSONAL
Do you compare yourself to others in your classes? If you do, do you feel you are closer to viewing it as healthy motivation or more crippling stress?Irrational numbers are stored as floating point numbers with a finite number of decimal places. This means that the values are not completely exact, and could cause some round-off errors, as demonstrated by calculating sine of pi, which returned some number to the power of -17, which is basically 0. This means that when dealing with numbers like this, it’s important to not directly test for equality (ex. If np.sin(np.pi) == 0) but instead round the numbers. I’ve read in a book somewhere about an equation to test equality while taking into account of round-off errors, but I can’t exactly remember that.
As for lists vs arrays, lists are definitely more versatile, such as appending and popping out elements, allowing the others to shift. Lists can also hold values of any type, while arrays are restricted to one data type for the entirety of the array. Lists are more flexible, so they can be used for a variety of purposes as storing a changing array. Arrays on the other hand are much better for data manipulation and calculation, such as for applying changes to every element in the array, or having a built in function to calculate the average.
It’s inevitable that there is some comparison going on, although not too much. I see it mainly as motivation, such as hearing about other people finishing their APUSH homework while I haven’t even started on it yet.
Week 3
Monday, July 24
ACADEMIC
How have prime and/or perfect numbers been applied in novel situations? Do you think there are perfect numbers that are odd?
(OPTIONAL) Prove why 2n(2n+1 - 1) will always generate a perfect number when (2n+1 - 1) is prime.
PERSONAL
What are your thoughts about writing journals? Do you think it is an effective way to learn?Prime numbers are used in cryptography which involves finding prime factors (I think). There isn’t solid proof for the existence of odd perfect numbers, and it relies on whether the converse of Euclid’s rule is true (all perfect numbers can be written as 2n(2n+1-1) where (2n+1-1) is prime). As of now, it is uncertain whether odd perfect numbers exist.
To prove the formula, we first have to write out the sum of all the factors. This only works when the other factor is prime, which allows us to split it into two sections: ones that involve the prime factor, and ones that do not. The factors without the prime portion consist of 1, 2, 4, 8, all the way up to 2n. The factors with the prime portion consist of 1 * prime, 2 * prime, all the way up to 2n-1 * prime, since adding 2n * prime is the number itself and thus cannot be used. After establishing that the factors add to the sum of the series (2n) + (2n-1)*(2n+1-1), we can start converting them.
We first have to establish a rule. Notice that 1, 2, 4, 8(23) add up to 15, which is 1 away from 16(24). Through deduction, we can see that sum from k = 0 to n of 2k is equal to 2n+1-1. This can also be proven through the formula of the sum of a geometric series, S = a(rn-1)/(r-1). The starting term is 1, which is 20, so the sum up to 2n should be up to the (n+1)th term. Thus, S = 1(2n+1-1)/(2-1) = 2n+1-1.
Now that it’s established, let’s convert 2n to 2n+1-1.
2n+1-1 + (2n-1) * (2n+1-1) = (2n-1+1)(2n+1-1).
By applying the same rule to 2n-1, it’s equal to 2n-1.
(2n-1+1)(2n+1-1) = 2n(2n+1-1).
I think journals are pretty useful for keeping track of what we learned, and it is definitely effective. It will also be interesting rereading the journals after the program is over, and get to see and remember what we did.
Tuesday, July 25
How might someone utilize or adapt something you saw at the Exploratorium for a robotics design project? Did something you saw specifically help shape your project?There are lots of different exhibits that people can utilize to help out with their robotics design. The ones that can help the most are probably the ones that employ mechanical devices like converting rotational force to lateral force, which would definitely come in handy when building robots. Nothing really changed much of the design, since ours was already planned out.
I have given up on jounals from this point forward ❤
BioPhysics
Week 1
Week 1 wasn't that exciting. It was mostly learning and review of python basics, and there's not much to show here, unfortunately :(
Week 2
We started getting into more advanced topics this week. We explored plotting programs and learned about probability, creating a couple of simulations for the problems as well to verify the math.While experimenting with the graphing software, I created a couple of pretty cool and interesting graphs based on polar equations and variations in the x and y coordinates (either random or trigonometrical for swirls), as shown below.Getting on to probability, the main focus was the problem of "Gambler's ruin". The basic principle is as follows: two players, p1 and p2, each starts with a certain amount of money, m1 and m2. Every "step", a coin is flipped (let's call the probability of player 1 winning p), and the winning side takes 1 unit of money from the other. The game continues until one goes completely bankrupt.
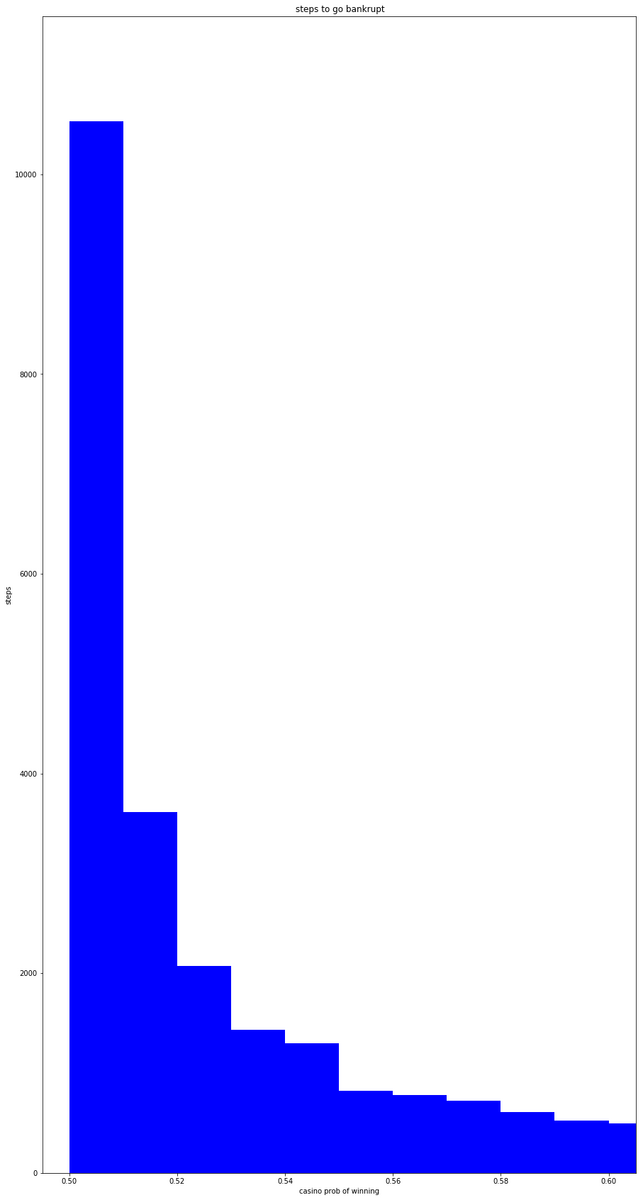
This problem presented many different trials and experiments, as shown below.The first is a graph of the number of steps it takes for player 1 to win in an unfair game favored towards player 1 (p=0.6). They both start with $50, and it takes around 250 turns for player 1 to win all of the money from player 2, which is surprisingly high in my opinion with the skewed probability.The next is a plot of the compounded win percentage of a fair game, with a probability of 0.5. The win percentages are compounded up, which means that at 40 simulations, the win percent is that of the first 40 trials, and at 80 simulations it is that of the first 80, including the previous 40. What this graph shows is how the probability eventually smoothes out to around 0.5, which is what is expected.The super long image is a graph of how many steps it takes to bankrupt a person with $100 playing against a casino with $10,000, and just minor variations in the win probability (skewed to the casino) can affect how many steps it takes to bankrupt.
Now that we have represented the problem graphically, how can we solve it analytically?Let's first calculate the probability of a player winning based on their starting money, assuming it is a fair game.We can consider the problem as a number line from the perspective of p1: initial value is 0, meaning neither side had won any money yet. The left boundary is -m1, while the right is m2. The point moves along the axis as either side wins or loses. Player 1 winning moves it to the right, increasing its value, and losing is vice versa.Now, let's represent the probability of reaching either side starting at position x as P(x). We can define this function recursively: the probability of arriving at x is 1/2 * (P(x-1) + P(x+1)). Through some magic and math, we can determine the function as linear, representable as A*x + B.Now that that's established, let's consider the end options. What if our point starts at -m1, aka P(-m1)? This means that p1 is already bankrupt, and the probability of p1 winning is 0. Thus, P(-m1) = 0. By the same logic, P(m2) would return 1.Since we know P(-m1) = 0, we can further refine our equation for P as A(x+m1), since when x = -m1, P = 0. Plugging in the other case, substituting P = 1 and x = m2, we get A = 1/(m1 + m2). Putting it all together, P = (x + m1) / (m1 + m2).. Since we're starting at x = 0, P = m1 / (m1 + m2), which is the ratio of the player's money to the collective amount of money.To solve for the average amount of steps for one to go bankrupt, the steps T can be defined recursively again as well. We define T(x) as 1/2 * (T(x-1) + T(x+1)) + 1, with the added one being the step it is currently on. This apparently results in a quadratic equation in the form A * x^2 + B * x + C.If we consider the cases of T(-m1) and T(m2), the game already ends the moment it starts, so the time is 0. Plugging this into the equation using the two intercepts, we get T = (x + m1) * (m2 - x). Subsituting in x = 0, we get T = m1 * m2.These calculated results may seem surprising, but they were verified by running tons of simulations and calculating the values.
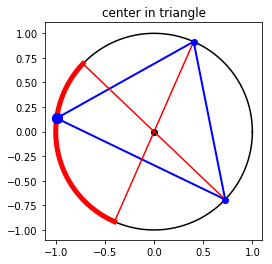
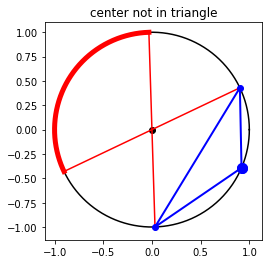
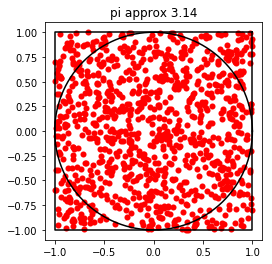
Below these, I have also added some other random probability simulations just for fun!The ones with the circle is a pretty famous problem: create a triangle by choosing 3 points, A, B, C, on a circle. What is the probability that this triangle includes the center point?The way I brute forced it was by calculating the opposite points of A and B, and generate the shorter arc in between them (in red). If point C is within that arc, then the triangle will cover the center.Although the logic was flawless, implementing took lots of trial and error, revolving around the circular nature of the perimeter coordinates.After it was all working, the simulation data produced a convincing probability: 25%.Another simulation is for calculating the value of pi, by simply randomly generating dots on a 2x2 square. The dots that land within the enclosed circle of radius 1 compared to the ratio of all the darts generated should be pi/4 (area of circle divided by square). After running through calculations and simulations, the value of pi was determined to be around 3.14.

polar graph

polar graph

polar grapgh (cos(4θ))
polar graph (cos(4θ) modified)
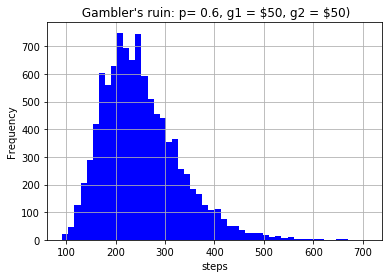
A simulation for gambler's ruin, favored towards player 1.
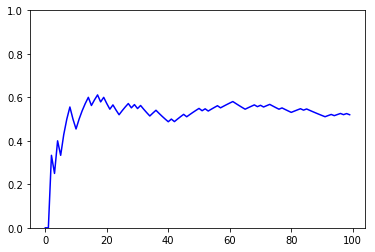
Compounded probability of one player winning a fair game
center in triangle
center not in triangle
calculating pi
How many steps it takes for the player to bankrupt against the bank
Week 3
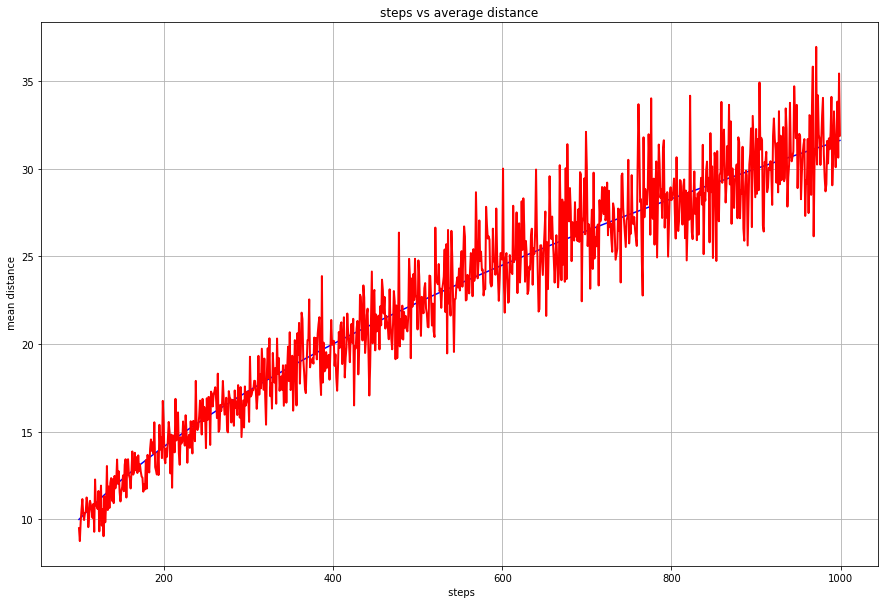
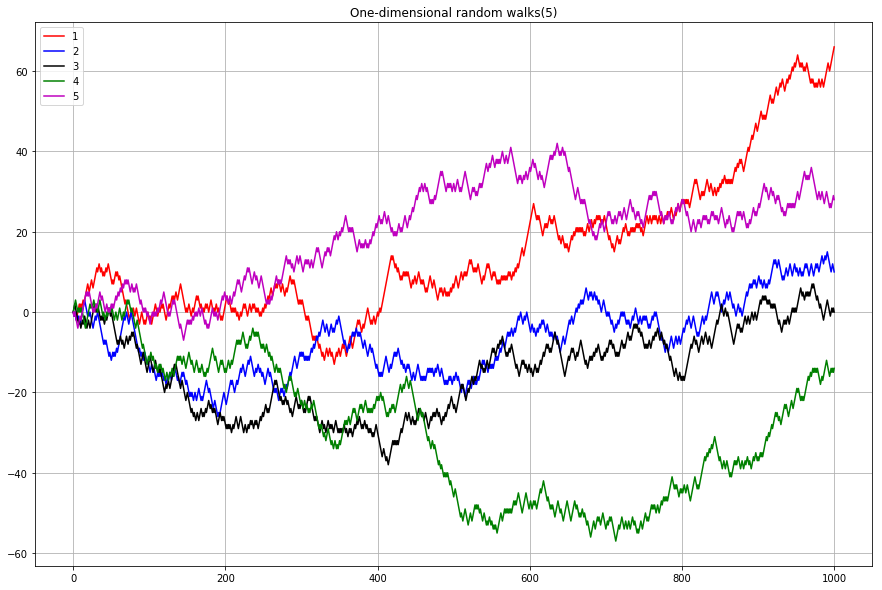
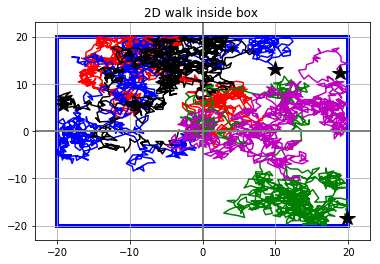
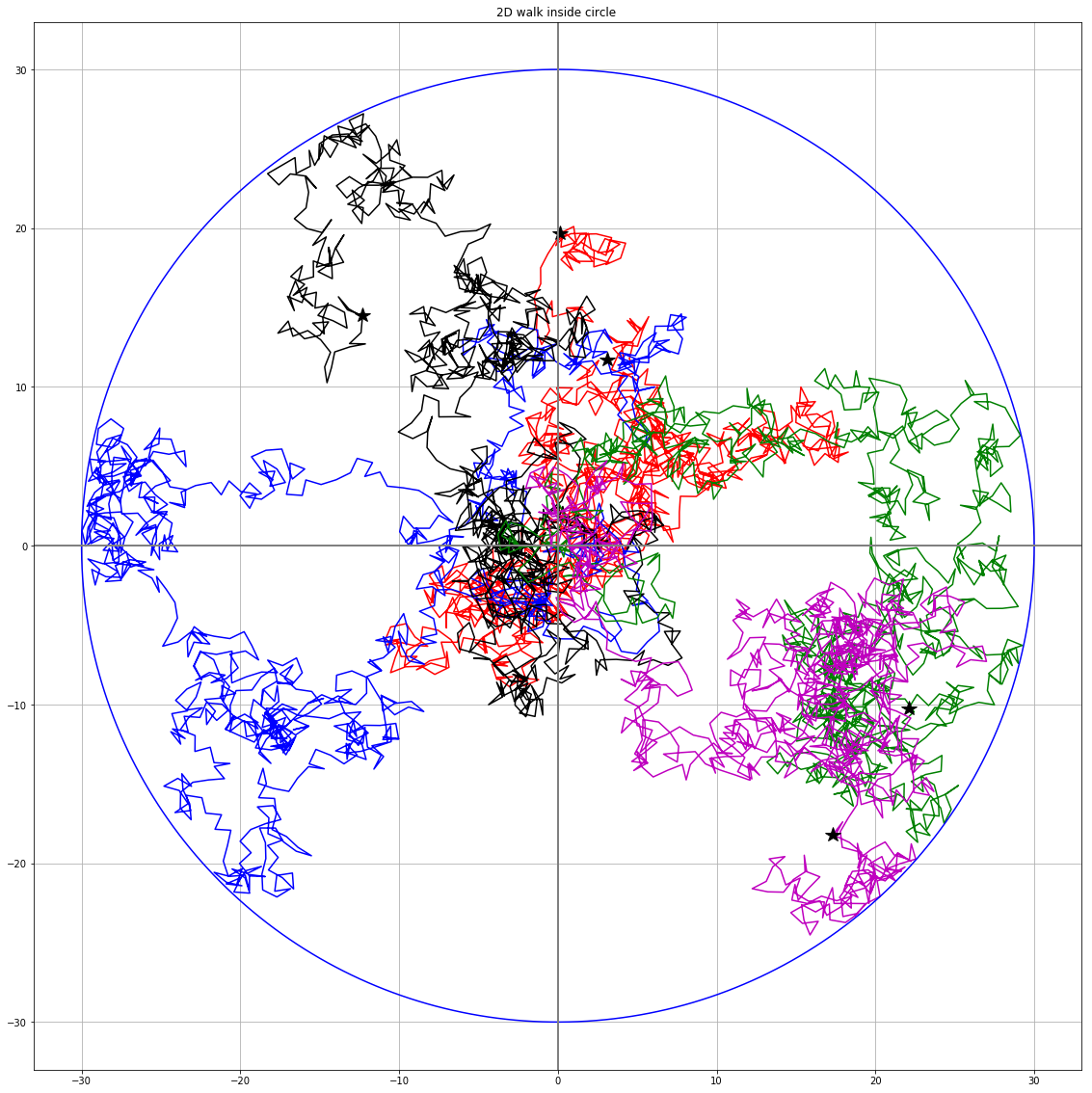
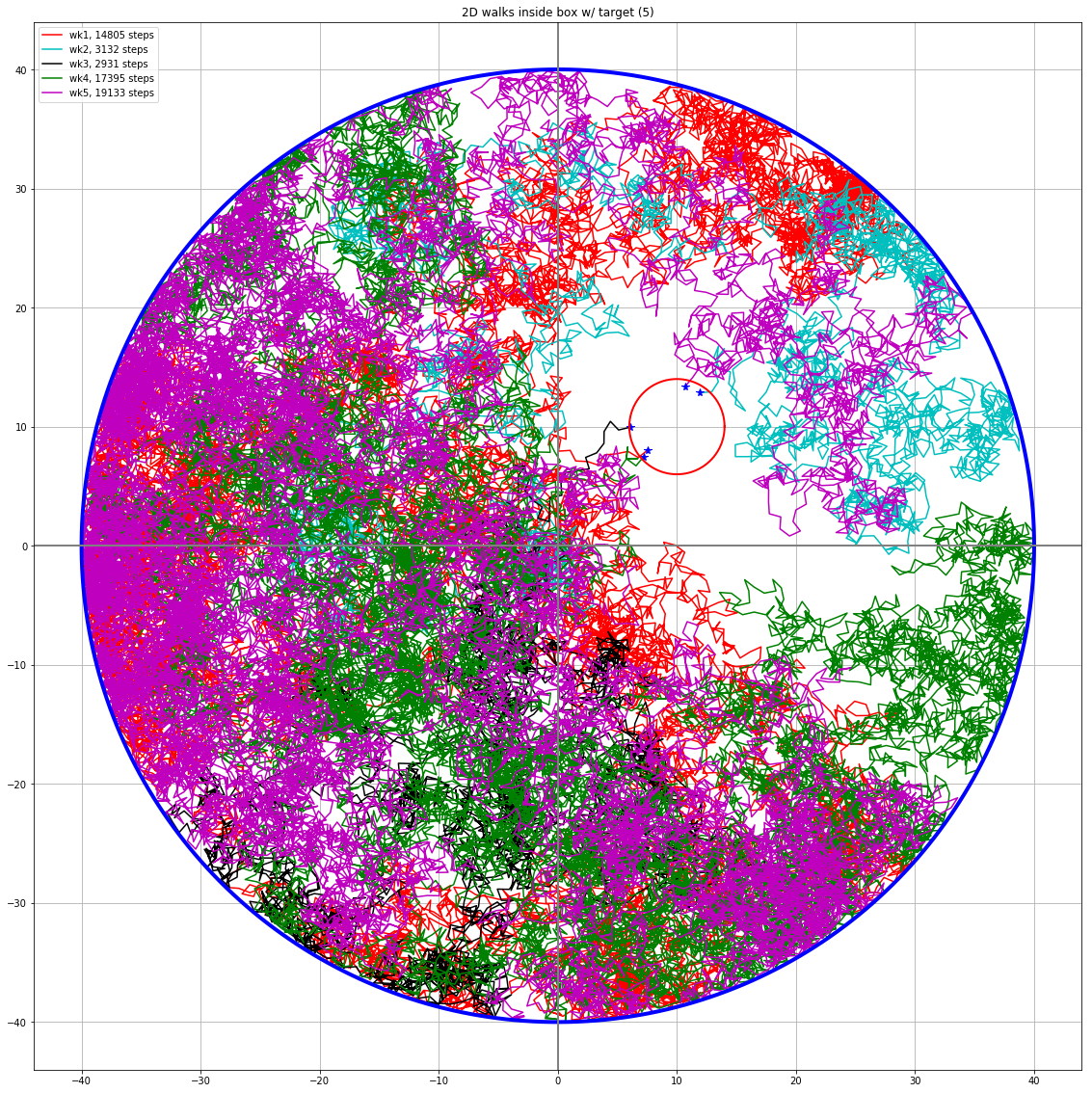
We really started getting into random walks (what the biophysics part is about) this week. We first modeled a 1D random walk with particles moving along a line randomly left and right.We simulated and graphed the endpoints of the 1D walks, which turned out to be a bell curve with the peak at 0 (the starting point), which makes sense since in a completely random movement moving left and right with equal probability, the most probable place to end up is where it started.One interesting fact was that the average distance (using RMS, root mean square, sqrt(avg(x^2))) of the particles form a square root relationship to the number of steps the particles took.We then moved on to creating 2D random walks, moving in random directions and later confining it into a boundary. We also created a simulation that simulates the time it takes for a random walker to reach a target.
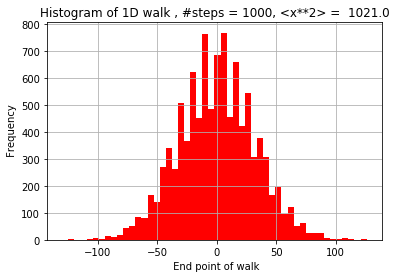
ending position of a 1D random walk
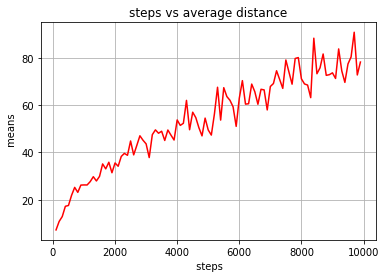
steps vs average distance from 0
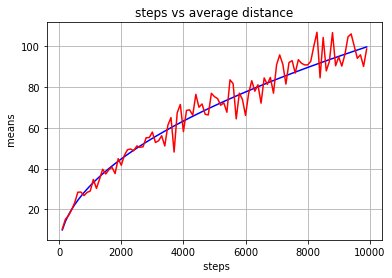
steps vs average distance, with sqrt(x) plotted

steps vs average distance, with sqrt(x) plotted

position of 1D walks

2D random walk with set steps within square boundary

2D random walk reaching target within square boundary

2D random walk with set steps within circular boundary

2D random walk reaching target within circular boundary
Week 4
The entirety of last week was working on the final project.We chose our final project on translating random RNA strings into amino acids. We hypothesized and tested many ideas that can be proven using the simulated data.The simulation is simple: random RNA sequences are generated, and it is iterated through and searched for a start codon. Once that is found, the program translates codon by codon down the string until the stop codon is found. It then continues to search for a start codon, and all of the resulting amino acid chains are then stored to be used later for analysis.I won't be rewriting everything so here is the link to the google collab:
collab notebook
Robotics
Week 1
Week one was mainly about the basics of computers and an introduction to the robots that we will use to create our final projects. Along with learning how to work with the robots, we also started reading Outsmart Your Brain, which gives lots of useful tips regarding learning.The robots were lego EV3 using C, which was relatively easy to learn with my Java experience. The entirety of this week was dedicated to learning how to control the robot through pre-programmed instructions instead of direct control, which was both fun sometimes but also frustrating due to the inaccurate nature of the movements.We did simple programs such as moving a specific amount of distance or turning precisely 90 degrees to familiarize ourselves with the syntax and functionality of the motors, which would definitely come in handy later on.

robot going around obstacle course

chassis for final project, boba bot
Week 2
Week 2 picked back up with the obstacle course, which we struggled on for 2 or three days. Right after that, we started on using the color sensors for following lines and identifying colors to play different sounds. That was the part that everyone was stuck on for a good 3 days, mainly because of the inconsistencies of the colors due to lighting differences as well as the close values of the colors of the different types of tape. We were able to complete it despite all the frustration, and we were able to get a start on our final project robot, the boba bot.